마르코프 결정 과정(Markov Decision Process, MDP)
일반적인 RL은 마르코프 결정 과정으로 기술 가능하다.
MDP를 푸는 기본적인 방법은 동적계획법(Dynamic Programming)이다.
동적계획법(Dynamic Programming)
컴퓨터 알고리즘으로 재귀적인 문제 해결에 관한 것으로 비교적 복잡한 문제를 작은 하위 문제로 나누어서 해결한다.
동적계획법은 재귀와 달리 하위 문제의 결과를(보통 딕셔너리나 룩업(lookup)테이블 형태로)저장하여 다시 맞닥뜨렸을 때
다시 계산하지 않고, 일정시간(constant time) 안에 다시 참조할 수 있다.
RL은 동적계획법에 비해 몇 가지 장점을 가지며 마르코프 결정 과정을 수행할 수 있다.
(동적계획법은 상태 크기(가능한 상황의 수)가 커지면 적용하기 어렵다.)
동적계획법으로 처리하기 큰 문제는 RL을 사용해서 훨씬 효과적이고 실용적으로 해결할 수 있다.
MDP(Markov Decision Process)
{s_t, a_t, r_t+1}
s_t: t에서의 상태
a_t: t에서의 선택한 행동
r_t+1: a_t에 대한 보상
s, r, a는 사전에 정의된 유한한 집합에서 값을 선택한다.
s와 r은 이전 타입 스텝에만 의존하는 확률 분포
위 확률 분포는 환경의 동역학(dynamics)또는 환경 모델을 완벽하게 정의
(모든 환경의 전이 확률(transition probability)를 계산가능)
환경 동역학이 필요하거나 학습하는 강화학습 방법을 모델 기반(model-based) 방법이라고 한다.
(환경 동역학을 사용하지 않는 강화학습 방법을 모델 프리(model-free) 방법이라고 함)
model-free & model-based
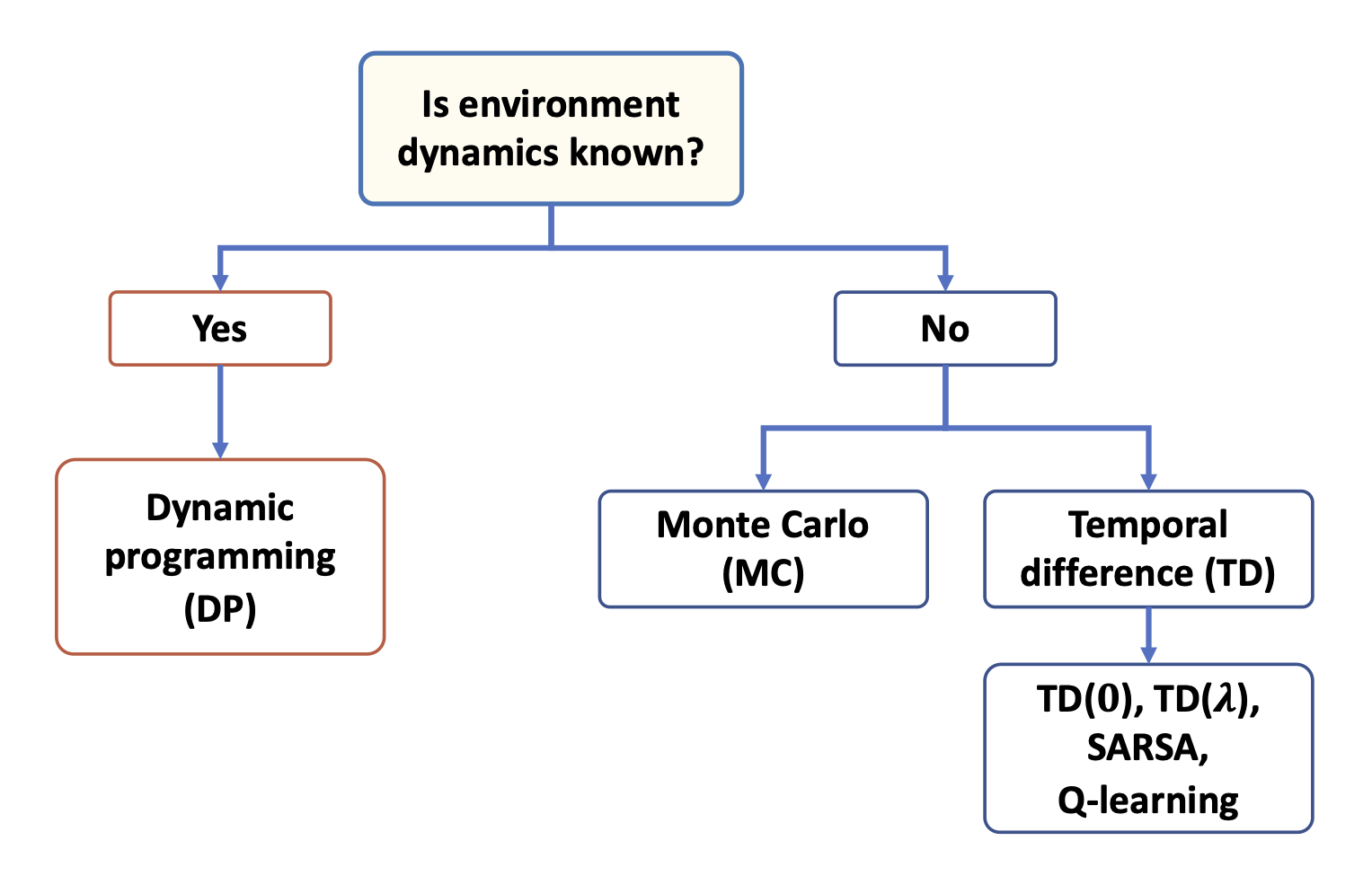
확률 p(s’, r | s, a)를 알고 있다면, 동적 계획법으로 학습 문제를 풀 수 있다.
실제 세상의 많은 문제처럼 환경 동역학이 알려지지 않았다면, 환경과 상호 작용을 통해 많은 수의 샘플을 수집해야 한다.
model-free
모델 프리를 다루기 위해서 다루는 두 가지 방법은 몬테카를로(Monte Carlo, MC)와
시간 차(Temporal Difference, TD) 방법이다.
p(s’, r|s, a)가 0, 1일 경우 즉 특정 행동이 항상 선택되거나 절대 선택되지 않는다면 환경 동역학이 결정적이다.
하지만 일반적으로 환경은 확률적으로 움직인다.
가능한 모든 보상을 합하는 식으로 주변 확률(marginal probability)를 계산할 수 있다.
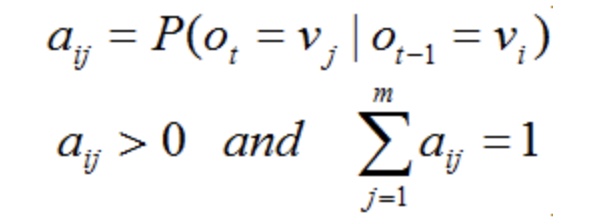
상태-전이 확률에 기반하여 환경 동역학이 결정적이라면, 에이전트가 상태 S_t=s, 행동 A_t=a을 선택할 때,
다음 상태 S_t+1=s’로 전이할 확률이 100%가 된다. p(s’|s, a)=1
ex)


마르코프 과정 시각화
유향 순환 그래프(directed cyclic graph)를 통해서 마르코프 과정을 표현
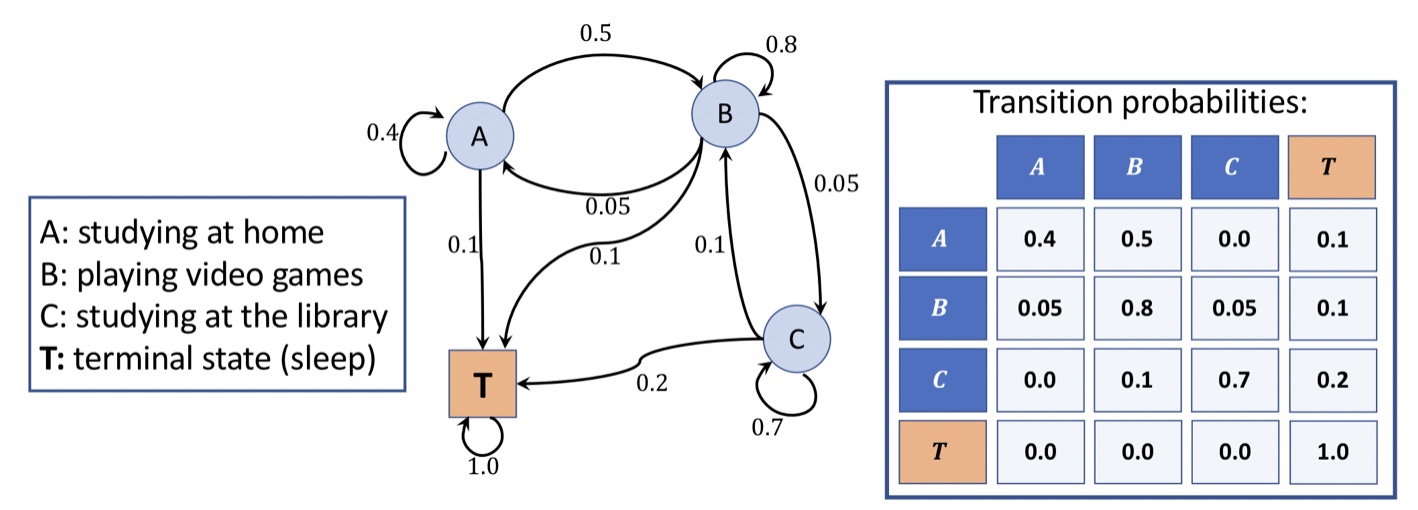
그래프의 에지(edge)(노드간의 연결)는 상태 간의 전이 확률을 나타낸다.
(행의 한 상태에서 다른 상태(노드)로 전이할 확률의 합은 항상 1이다)
에피소드 작업 & 연속적인 작업
에이전트가 환경과 상호 작용함에 따라 관측이나 상태의 시퀀스는 궤적(trajectory)을 형성한다.
에이전트의 궤적은 시간 t=0에서 시작해서
t=T에서 끈타는 부분 궤적으로 나눌 수 있다면 에피소드 작업(episode task)라고 하고,
종료 상태가 없어 끝없이 궤적인 계속되면 연속적인 작업(continuing task)라고 한다.
체스 게임을 위한 에이전트를 학습하는 것은 에피소드 작업이고,
청소 로봇은 연속적인 작업을 수행한다.